جدول المحتويات:
- الخطوة 1:
- الخطوة 2:
- الخطوة 3: مخطط الجهد والتيار لأشكال الموجة
- الخطوة 4: زوايا طور التيار والمقاومة والجهد لدارات RC المتوالية
- الخطوة 5: المقاومة وزاوية الطور لدارات RC المتوالية
- الخطوة 6: تغيير الممانعة بالتردد
- الخطوة 7: تغيير الممانعة وزاوية الطور مع التردد
- الخطوة 8: رسم توضيحي لكيفية تغير Z و XC مع التردد
- مؤلف John Day [email protected].
- Public 2024-01-30 07:36.
- آخر تعديل 2025-01-23 12:53.

دوائر RC
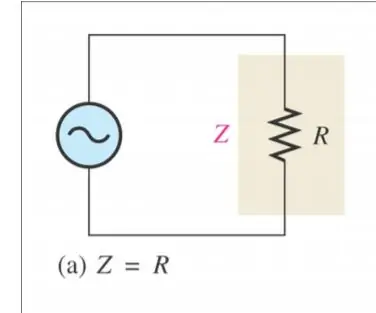
المقاومة: هي ما "يرى" المصدر أنه معارضة تامة للتيار
تختلف طريقة حساب الممانعة عن دائرة واحدة
الخطوة 1:

عندما تكون الدائرة بالسعة البحتة (تحتوي على مكثف فقط) ، تكون زاوية الطور بين الجهد المطبق والتيار الكلي 90 درجة (الموصلات الحالية)
الخطوة 2:

عندما يكون هناك مزيج من المقاومة والسعة في الدائرة ، تكون زاوية الطور بين المقاومة (R) والمفاعلة السعوية (XC) 90 درجة وزاوية الطور للمقاومة الكلية (Z) في مكان ما بين 0 درجة و 90 درجة
عندما يكون هناك مزيج من المقاومة والسعة في الدائرة ، تكون زاوية الطور بين التيار الكلي (IT) والجهد المكثف (VC) 90 درجة وزاوية الطور بين الجهد المطبق (VS) والتيار الكلي (IT) في مكان ما بين 0 درجة و 90 درجة ، اعتمادًا على القيم النسبية للمقاومة والسعة
الخطوة 3: مخطط الجهد والتيار لأشكال الموجة

الخطوة 4: زوايا طور التيار والمقاومة والجهد لدارات RC المتوالية

الخطوة 5: المقاومة وزاوية الطور لدارات RC المتوالية

- في دائرة RC المتسلسلة ، تكون الممانعة الإجمالية هي مجموع طور R و Xc
- مقدار المعاوقة: Z = √ R ^ 2 + Xc ^ 2 (مجموع المتجهات)
- زاوية الطور: θ = tan-1 (X C / R)
لماذا نستخدم المتجه المجموع وليس المجموع الجبري؟
الإجابة: لأن المقاومة لا تؤخر الجهد ، لكن المكثف يفعل ذلك.
لذا ، Z = R + Xc خطأ.
يتضمن تطبيق قانون أوم على دائرة RC سلسلة كاملة استخدام الكميات Z و Vs و Itot على النحو التالي:
Itot = Vs / Z Z = Vs / Itot Vs = Itot * Z
لا تنس أيضًا:
Xc = 1/2 FC
الخطوة 6: تغيير الممانعة بالتردد

الخطوة 7: تغيير الممانعة وزاوية الطور مع التردد

الخطوة 8: رسم توضيحي لكيفية تغير Z و XC مع التردد

يبقى R ثابتًا
موصى به:
مقدمة عن دوائر الأشعة تحت الحمراء: 8 خطوات (بالصور)

مقدمة إلى دوائر الأشعة تحت الحمراء: الأشعة تحت الحمراء هي قطعة معقدة من التكنولوجيا ولكن من السهل جدًا التعامل معها. على عكس المصابيح أو الليزر ، لا يمكن رؤية الأشعة تحت الحمراء بالعين البشرية. في هذا Instructable ، سأوضح استخدام الأشعة تحت الحمراء من خلال 3 دوائر مختلفة. لن تكون الدوائر
دوائر تخطيط كهربية القلب في التوابل LT: 4 خطوات

ECG Circuitry في LTspice: قم بتنزيل LTspice لأي من أجهزة Mac أو الكمبيوتر الشخصي. تم عمل هذا الإصدار على جهاز Mac
ثلاث دوائر لمكبرات الصوت -- البرنامج التعليمي خطوة بخطوة: 3 خطوات

ثلاث دوائر لمكبرات الصوت || برنامج تعليمي خطوة بخطوة: تعمل دائرة مكبر الصوت على تقوية الإشارات الصوتية التي يتم استقبالها من البيئة إلى الميكروفون وإرسالها إلى مكبر الصوت من حيث يتم إنتاج الصوت المضخم ، وهنا ، سأوضح لك ثلاث طرق مختلفة لجعل دائرة مكبر الصوت هذه باستخدام:
دوائر MakeyMakey: 3 خطوات
دوائر MakeyMakey: نمزج في الجدول لوحًا مصنوعًا ، وبعض أسلاك التمساح وبعض الأشياء الموصلة للكهرباء. مع بعض المشاريع التفاعلية في البداية ، نبني دوائر للتفاعل مع الكمبيوتر و / ومع الكائنات
اختر بدائل المستشعر في دوائر Tinkercad: 3 خطوات (بالصور)
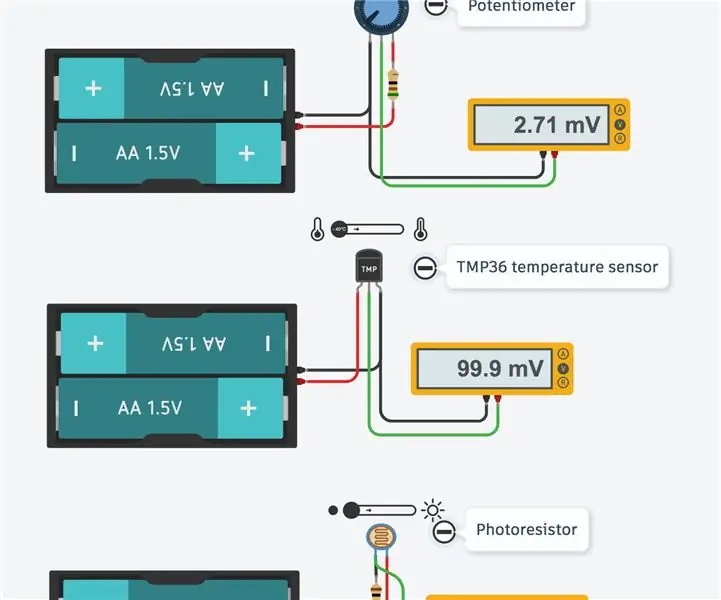
اختر بدائل الاستشعار في دوائر Tinkercad: حسب التصميم ، تحتوي Tinkercad Circuits على مكتبة محدودة من المكونات الإلكترونية شائعة الاستخدام. يجعل هذا التنظيم من السهل على المبتدئين التنقل في تعقيد عالم الإلكترونيات دون الشعور بالارتباك. الجانب السلبي هو أنه إذا
