
جدول المحتويات:
- مؤلف John Day [email protected].
- Public 2024-01-30 07:36.
- آخر تعديل 2025-01-23 12:53.


هنا تطبيق عملي لمعادلات الرياضيات المعقدة.
هذه في الواقع تقنية مفيدة للغاية يمكنك استخدامها لوصف المكونات ، أو حتى الهوائي ، بترددات محددة مسبقًا.
إذا كنت تتلاعب بالإلكترونيات ، فقد تكون على دراية بالمقاومات وقانون أوم. R = V / I قد تتفاجأ الآن بمعرفة أن هذا هو كل ما تحتاجه لحل مشكلة المعاوقة المعقدة أيضًا! جميع الممانعات معقدة بشكل أساسي ، أي أنها تحتوي على جزء حقيقي وخيالي. في حالة المقاوم ، يكون التخيل (أو المفاعلة) 0 ، وبالتالي لا يوجد فرق طور بين V و I ، لذلك يمكننا استبعادهم.
ملخص سريع للأعداد المركبة. يعني المركب ببساطة أن الرقم يتكون من جزأين ، حقيقي وخيالي. هناك طريقتان لتمثيل الأعداد المركبة ، على سبيل المثال في الشكل أعلاه ، يمكن تحديد نقطة بالقيم الحقيقية والخيالية ، مثل مكان التقاء الخطين الأصفر والأزرق. على سبيل المثال ، إذا كان الخط الأزرق عند 4 على المحور X ، و 3 على المحور Y ، فسيكون هذا الرقم 4 + 3i ، فأنا يشير إلى أن هذا هو الجزء التخيلي من هذا الرقم. هناك طريقة أخرى لتحديد نفس النقطة وهي طول (أو سعة) الخط الأحمر وكذلك الزاوية التي يصنعها مع الأفقي. في المثال أعلاه سيكون 5 <36.87.
أو خط طوله 5 بزاوية 36.87 درجة.
في المعادلة أعلاه جميع المعلمات ، يمكن اعتبار R و V وأنا على أنها جزء وهمي ، عند العمل مع المقاومات هذه القيمة هي 0.
عند العمل مع المحاثات أو المكثفات ، أو عندما يمكن قياس فرق الطور (بالدرجات) بين الإشارات ، تظل المعادلة كما هي ولكن يجب تضمين الجزء التخيلي من الرقم. تجعل معظم الآلات الحاسبة العلمية من التعامل مع الرياضيات المعقدة أمرًا سهلاً للغاية ، وسأعمل في هذا البرنامج التعليمي من خلال مثال على Casio fx-9750GII.
أولاً ، ملخص لمعادلة مقسم جهد المقاوم.
حسب الشكل -
الجهد عند Y هو التيار i مضروبًا في R2
i هو الجهد X مقسومًا على مجموع R1 و R2
عندما تكون R2 غير معروفة ، يمكننا قياس القيم الأخرى ، X ، Y ، R1 وإعادة ترتيب المعادلة لحل R2.
اللوازم
آلة حاسبة علمية
مولد الإشارة
راسم الذبذبات
الخطوة 1: الإعداد

لنفترض أننا نريد حساب محاثة الجهاز قيد الاختبار (DUT) عند 1 ميجا هرتز.
تم تكوين مولد الإشارة لإخراج جيبي يبلغ 5 فولت عند 1 ميجا هرتز.
نحن نستخدم مقاومات 2 كيلو أوم ، وقنوات الذبذبات هي CH1 و CH2
الخطوة الثانية: راسم الذبذبات

نحصل على أشكال الموجة كما هو موضح في الشكل. يمكن رؤية تحول الطور وقياسه على مرسمة الذبذبات ليكون رائدًا بمقدار 130 نانومتر. السعة 3.4 فولت. لاحظ أن الإشارة على CH1 يجب أن تكون 2.5 فولت حيث يتم أخذها عند خرج مقسم الجهد ، وهنا تظهر على أنها 5 فولت من أجل الوضوح ، لأن هذه هي القيمة التي يجب أن نستخدمها أيضًا في حساباتنا. أي 5V هو جهد الدخل للمقسم مع المكون غير المعروف.
الخطوة 3: حساب المرحلة

عند 1 ميجاهرتز ، تكون فترة إشارة الإدخال 1us.
130ns يعطي نسبة 0.13. أو 13٪. 13٪ من 360 هي 46.6
تُعطى إشارة 5V بزاوية 0.. لأن هذه إشارة دخلنا وانزياح الطور متعلق بها.
تُعطى إشارة 3.4V الزاوية +46.6 (+ تعني أنها تقود ، بالنسبة للمكثف ستكون الزاوية سالبة).
الخطوة 4: في الآلة الحاسبة


الآن نقوم ببساطة بإدخال القيم المقاسة في الآلة الحاسبة.
R تساوي 2 كيلو
V تساوي 5 (EDIT - V تساوي 5 ، لاحقًا في المعادلة تستخدم X! النتيجة هي نفسها تمامًا كما كان لدي X مثل 5 في الآلة الحاسبة)
Y هو الجهد المقاس بزاوية الطور ، ويتم إدخال هذا الرقم كرقم مركب ، ببساطة عن طريق تحديد الزاوية كما هو موضح في شاشة الآلة الحاسبة
الخطوة 5: حل المعادلة

الآن المعادلة
(ص * ص) / (س - ص)
في الآلة الحاسبة ، هذه بالضبط نفس المعادلة التي نستخدمها لحل فواصل جهد المقاوم:)
الخطوة 6: القيم المحسوبة


أسفرت الآلة الحاسبة عن النتيجة
18 + 1872 ط
18 ، هو الجزء الحقيقي من الممانعة ولها محاثة +1872 عند 1 ميجاهرتز.
والذي يعمل حتى 298uH وفقًا لمعادلة مقاومة المحرِّض.
18 أوم أعلى من المقاومة التي يمكن قياسها بمقياس متعدد ، وذلك لأن المتر المتعدد يقيس المقاومة عند التيار المباشر. عند 1 ميجاهرتز ، يوجد تأثير جلدي ، حيث يتم تجاوز الجزء الداخلي للموصل بواسطة التيار ويتدفق فقط على السطح الخارجي للنحاس ، مما يقلل بشكل فعال من منطقة تقاطع الموصل ، ويزيد من مقاومته.
موصى به:
كيف تحقق أي مقاومة / سعة باستخدام مكونات لديك بالفعل: 6 خطوات

كيفية تحقيق أي مقاومة / سعة باستخدام مكونات لديك بالفعل!: هذه ليست مجرد سلسلة أخرى / حاسبة مقاومة مكافئة موازية! يحسب هذا البرنامج كيفية الجمع بين المقاومات / المكثفات التي تحتاجها حاليًا لتحقيق قيمة مقاومة / سعة سعة مستهدفة تحتاجها. هل احتجت يومًا إلى مواصفات
إصدار الساعة المكون من 7 أجزاء 2: 4 خطوات

7 Segment Clock الإصدار 2: مرحبًا! بعد طلب من مستخدم Instructables بخصوص توفر تنسيق 12 ساعة ، استفدت من إجراء تغييرات مالية على المشروع الأصلي. أثناء استخدام الإصدار 1 شعرت بالحاجة إلى إنشاء إصدار مستقل ، لذلك جعلت من الممكن
كيفية اختيار أثر المكون الصحيح: 3 خطوات
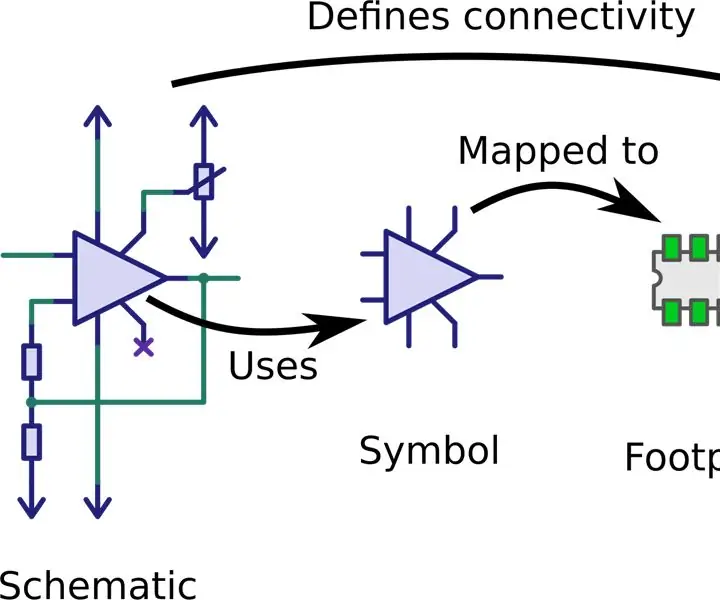
كيفية اختيار أثر المكون الصحيح: البصمة أو نمط الأرض هو ترتيب الفوط (في تقنية التثبيت على السطح) أو الثقوب (في تقنية الثقب) المستخدمة لربط المكونات فعليًا وتوصيلها كهربائيًا بلوحة دائرة مطبوعة . نمط الأرض على دائرة
MicroPython على لوحة مستشعر الفنون المعقدة: 3 خطوات

MicroPython على لوحة مستشعر الفنون المعقدة: أحد أكثر الجوانب المدهشة في متحكم ESP32 هو قدرته على تشغيل MicroPython. يمكن القيام بذلك بطريقتين: تشغيل برامج Python كاملة ، أو بشكل تفاعلي من خلال تطبيق وحدة التحكم. سيوضح هذا Instructable كيفية استخدام
استخدام لوحة مستشعر الفنون المعقدة للتحكم في البيانات النقية عبر شبكة WiFi: 4 خطوات (بالصور)

استخدام لوحة مستشعر الفنون المعقدة للتحكم في البيانات النقية عبر شبكة WiFi: هل سبق لك أن أردت تجربة التحكم بالإيماءات؟ اجعل الأشياء تتحرك بحركة من يدك؟ التحكم في الموسيقى بلمسة من معصمك؟ سيوضح لك هذا Instructable كيف! لوحة مستشعر الفنون المعقدة (complexarts.net) عبارة عن لوحة صغيرة
