تلخيص تكراري لمصفوفة في Java: 9 خطوات

2024 مؤلف: John Day | [email protected]. آخر تعديل: 2024-01-30 07:37

التكرار هو إجراء مفيد للغاية وفعال من حيث الوقت يمكنه حل مشكلة بسرعة باستخدام القليل جدًا من التعليمات البرمجية. تتضمن العودية الطريقة التي تنشئها للاتصال بنفسها لتقصير المشكلة الأصلية.

في هذا المثال ، سنجمع مصفوفة من 10 أعداد صحيحة ، لكن الحجم يمكن أن يكون بأي طول.

اللوازم

يجب أن تعرف بناء جملة جافا الأساسي وأن يكون لديك IDE أو محرر نصوص لكتابة التعليمات البرمجية الخاصة بك لهذه المهمة.

الخطوة 1: قم بإعداد طريقتك الرئيسية

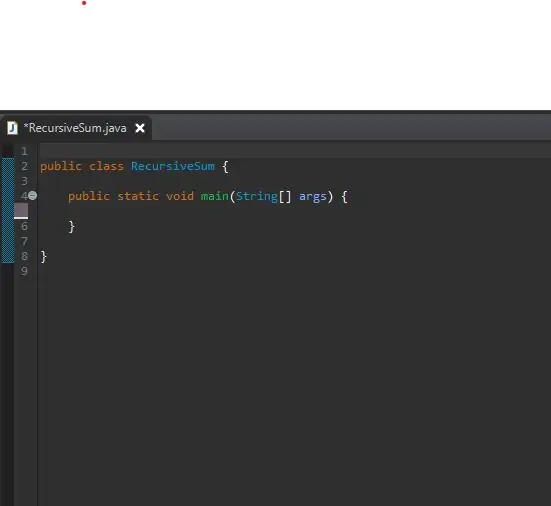
للبدء ، قم بإعداد طريقتك الرئيسية في فصل دراسي تم إنشاؤه حديثًا. لقد سميت صفي RecursiveSum. هذا هو المكان الذي ستنشئ فيه مصفوفة الأعداد الصحيحة وتستدعي الطريقة العودية.

الخطوة 2: قم بإنشاء رأس الطريقة العودية

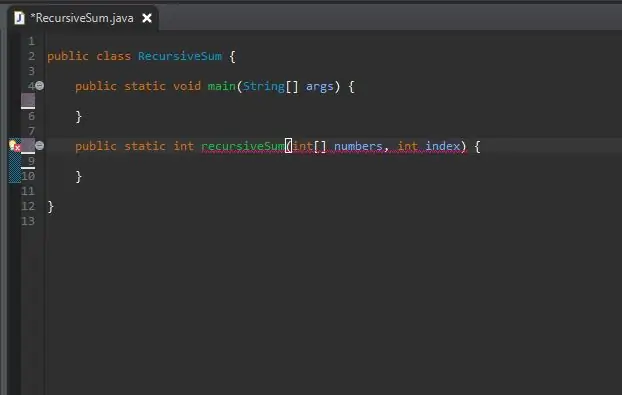
خارج طريقتك الرئيسية ، قم بإنشاء رأس الطريقة للطريقة العودية.

الطريقة ثابتة ، حيث إنها لن تتطلب كائنًا لاستخدامها عليها.

نوع الإرجاع هو int ، لأن المصفوفة التي سنستخدمها ستكون ممتلئة بالأعداد الصحيحة. ومع ذلك ، يمكن تغيير هذا إلى أي رقم يحتوي على المصفوفة.

لقد قمت بتسمية الأسلوب recursiveSum الخاص بي والذي سيأخذ معاملين ؛ مصفوفة من الأعداد الصحيحة والفهرس الذي سنضيفه إلى المجموع. لقد استدعيت هذه المعلمات أرقام والفهرس على التوالي.

سترى أخطاء الآن وهذا جيد. سيتم إصلاحها لاحقًا.

الخطوة 3: قم بإنشاء حافظة Kicker / Base الخاصة بك

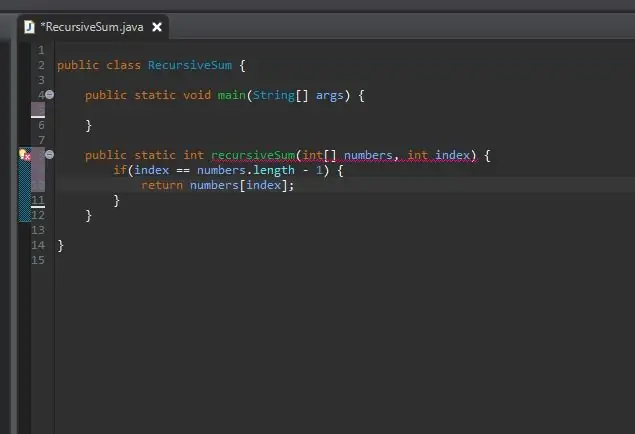
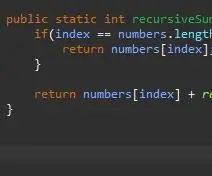
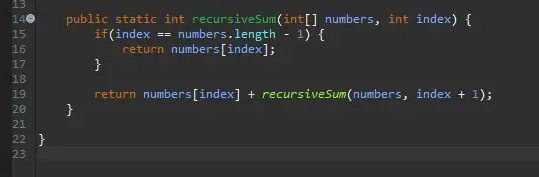
تحتاج الطريقة العودية إلى حالة قاعدية / أساسية. هذا هو الشرط الذي سيوقف طريقتك من استدعاء نفسها بلا حدود. يمكن اعتبار هذه الحالة الأساسية أبسط حالة سنواجهها. في هذه الحالة ، ستكون الحالة الأساسية عندما نكون في نهاية المصفوفة. إذا كان الفهرس الحالي يساوي طول المصفوفة (ناقص 1 لأن المصفوفات تبدأ العد من 0 وليس 1) ، فنحن في النهاية ونعيد ببساطة هذا العنصر إلى ذلك الفهرس.

الخطوة 4: الخطوة العودية

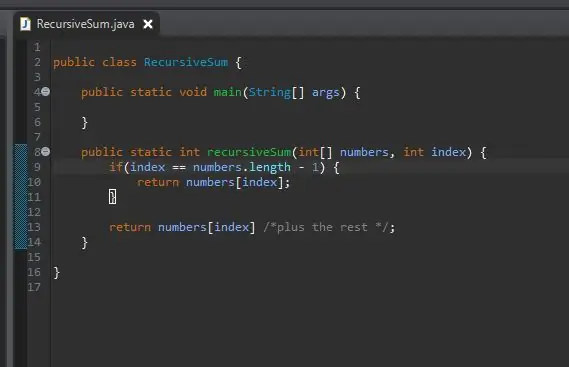
بمجرد أن نحصل على الحالة الأساسية ، فإن الخطوة التالية هي خطوتنا العودية. هذا هو المكان الذي يحدث السحر. لقد تعاملنا مع الحالة عندما يساوي الفهرس العنصر الأخير في المصفوفة. ماذا لو لم نكن في آخر عنصر في صفيفنا؟ ماذا لو تمكنا من إخبارها ببساطة بإضافة العنصر الحالي بالإضافة إلى العنصر التالي؟ في النهاية سنصل إلى نهاية المصفوفة الخاصة بنا وستصبح الحالة الأساسية الخاصة بنا سارية المفعول.

لتحقيق ذلك ، نقوم ببساطة بإرجاع فهرسنا الحالي و "إضافة الباقي" من المصفوفة.

الخطوة 5: تقصير المشكلة

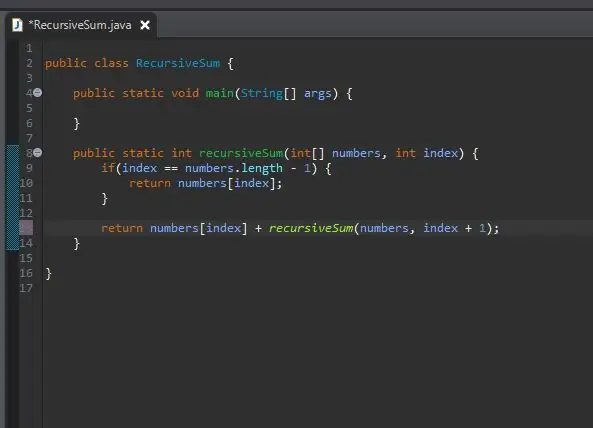
كيف يمكننا ببساطة "إضافة الباقي"؟ لدينا بالفعل طريقة تضيف عنصرًا معينًا ؛ لدينا طريقة recursiveSum ()! يمكننا تسميتها مرة أخرى ولكن تغيير الفهرس الذي نجمعه.

نمرر في نفس المصفوفة التي نعالجها ، لكننا نمرر الفهرس التالي من الفهرس الحالي. نقوم بذلك ببساطة عن طريق إضافة واحد إلى فهرسنا الحالي كما هو موضح.

الخطوة السادسة: إنشاء مصفوفة الأعداد الصحيحة

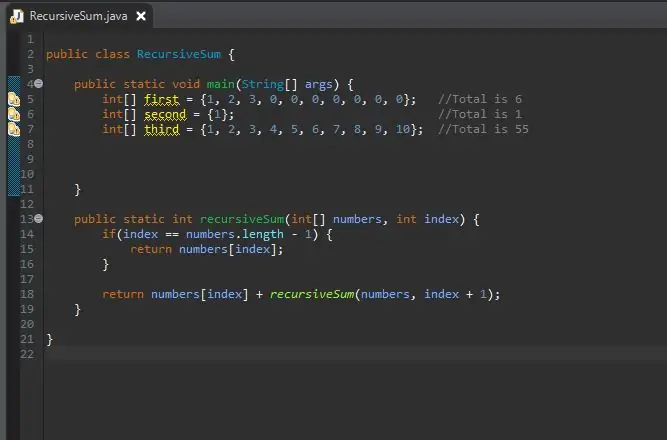
الآن بعد أن اكتملت طريقة الجمع العودية ، يمكننا إنشاء المصفوفة التي سنعالجها. ستكون هذه المصفوفة في كتلة الطريقة الرئيسية لدينا.

يمكنك جعل حجم المصفوفة طالما أردت. لقد أنشأت عددًا قليلاً من المصفوفات المختلفة بأحجام وقيم مختلفة لإظهار أنها لا تعمل على حجم واحد فقط.

الخطوة 7: استدعاء الطريقة مع المصفوفات الخاصة بك

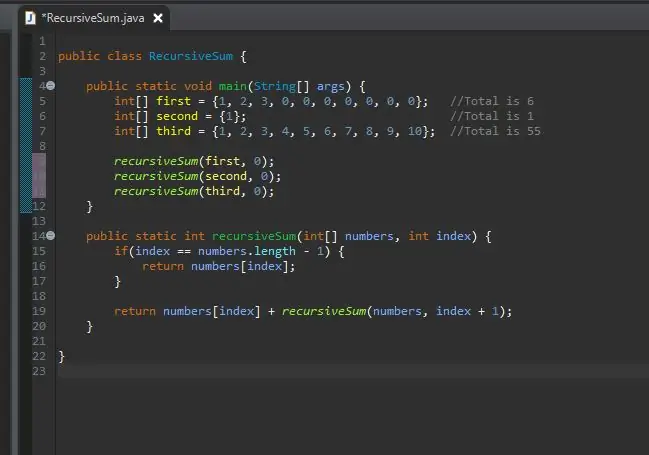
يمكنك الآن استدعاء طريقتك العودية وتمرير هذه المصفوفات إليها. الآن يمكنك تشغيل برنامجك.

الخطوة 8: اطبع النتائج

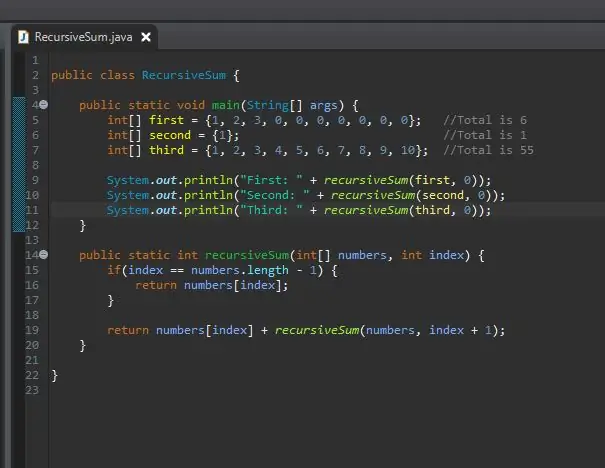
لم يحدث شيء. لماذا ا؟ يُرجع المجموع العودي عددًا صحيحًا ولكننا لم نقم بأي شيء بهذا العدد الصحيح. لقد قامت بعملها ولكن لا يمكننا رؤية النتيجة. لرؤية النتيجة ، نحن ببساطة نطبعها هكذا. بعد تشغيل هذا سترى النتائج لكل من المصفوفات الخاصة بك.

الخطوة 9: مبروك

لقد أكملت دالة تكرارية. لا تتردد في تغيير حجم المصفوفات الخاصة بك. إذا اختبرت ذلك ، فستلاحظ أنه يتعطل عندما يكون لديك مصفوفة فارغة. لم نأخذ في الحسبان ذلك ولكن هذه طريقة رائعة لتحسين طريقتك العودية.