هل تعرف عن تعديل ESP32 ADC ؟: 29 خطوة

2024 مؤلف: John Day | [email protected]. آخر تعديل: 2024-01-30 07:39

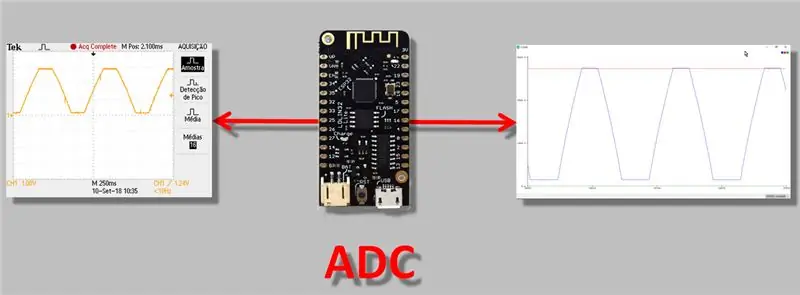
اليوم ، سأتحدث عن مشكلة أكثر تقنية ، ولكن أعتقد أن كل شخص يعمل مع ESP32 يجب أن يعرف: تعديل قراءة قضية ADC (المحول التناظري إلى الرقمي). أجد هذا مهمًا لأنه عند إجراء "قياس" ، خاصةً مع أداة لها إخراج تناظري ، يجب أن تكون متأكدًا تمامًا من أن القراءة يتم إجراؤها بشكل صحيح.

لذلك ، في الفيديو اليوم ، سنجري قياسات باستخدام "المحول التناظري الرقمي" الخاص بـ ESP32 ، ونلاحظ اختلافات التحويل ، ونطبق طريقة تعديل / معايرة ADC.

الخطوة 1: ما هو محول AD؟

محول AD عبارة عن دائرة قادرة على ترجمة كمية تناظرية (مستمرة) إلى قيم رقمية (منفصلة). ماذا يعني ذلك؟ هذا يعني أنه بينما لا يمكن للقيم الرقمية إلا أن تفترض القيم المنفصلة التي تتكون من مزيج من الأصفار والآحاد ، يمكن للكمية التناظرية أن تتحمل أي قيمة ضمن النطاق. على سبيل المثال ، إذا قمنا بقياس الجهد لخلية AA مثالية ، فيمكننا إيجاد أي قيمة بين 0V و 1.5V ، لأن هذه كمية تمثيلية. يجب أن تفترض حالة خرج المصباح المثالي حالتين فقط (إيقاف أو تشغيل) ، وهو مقدار منفصل. نظرًا لأن المتحكمات الدقيقة تعمل باستخدام هذا المنطق المنفصل ، فنحن بحاجة إلى دائرة قادرة على ترجمة الكمية التناظرية إلى رقمية (أو منفصلة).

الخطوة 2: الموارد المستخدمة

• بطاقة واحدة Lolin32 Lite v1.0.0

• راسم الذبذبات Tektronix TDS1001C للالتقاط

• كبل USB واحد لـ ESP32

• راسم الذبذبات Hantek DSO4102C كمولد إشارة

الخطوة 3: ESP32 ADC

وفقًا لبيانات Espressif ، قد تقدم رقائق ESP32 فرقًا +/- 6٪ من شريحة إلى أخرى في النتائج المقاسة.

بالإضافة إلى ذلك ، لا يحتوي التحويل على إجابة خطية لكل نطاق متاح للقراءة. يوفر Espressif طريقة للمعايرة ويقترح أن يقوم المستخدمون بتنفيذ طرق أخرى إذا رأوا أنه من الضروري تحقيق الدقة المطلوبة.

سنجري عملية الحصول على البيانات ، ومن هذا ، سنعرض ردود ADC ومثالًا لتطبيق عملية حسابية لقراءة التعديل.

هناك عدة طرق (أبسط أو أكثر تعقيدًا) لإنجاز هذه الإصلاحات. الأمر متروك لك لتقييم الأنسب لمشروعك.

سيكون للواحد الموضح هنا غرض توضيحي ومحاولة معالجة النقاط المثيرة للاهتمام التي يمكن ملاحظتها أثناء التعديلات.

الخطوة 4: الدائرة المستخدمة

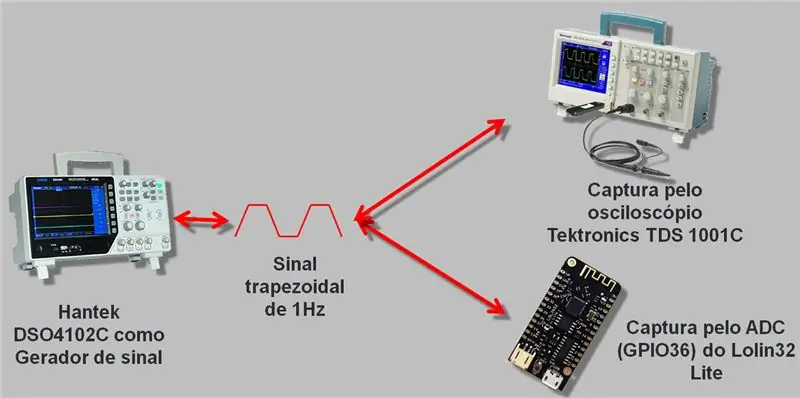
لقد استخدمت راسم الذبذبات مع مولد إشارة يصل إلى 25 ميجاهرتز ، وهو Hantek DSO4102C. قمنا بتوليد موجة تمت قراءتها بواسطة ESP A / D وراسم الذبذبات. تم تسجيل البيانات التي تم جمعها في ملف csv وفي جدول بيانات ، وسأتركه في نهاية المقالة للتنزيل.

الخطوة 5: تسجيل المستخدم

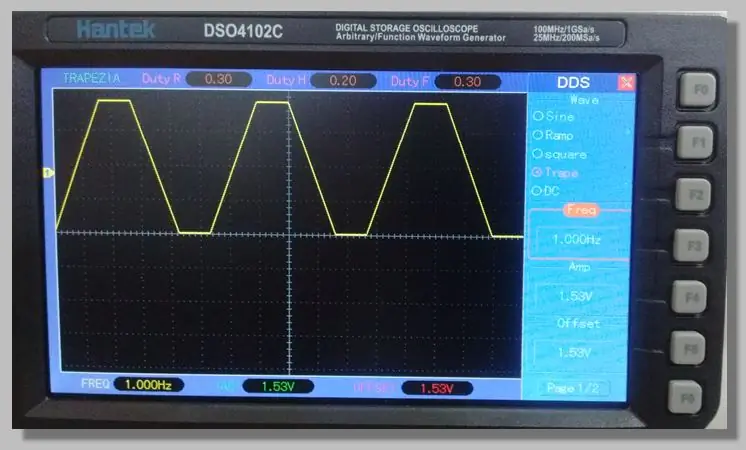
لقد اخترنا إشارة شبه منحرف منخفضة التردد تسمح بالوصول إلى المنحدرات التي تمر عبر نطاق التحويل بأكمله. هذا يسمح لعدد كبير من العينات على هذه المنحدرات.

الخطوة 6: البيانات التي تم الحصول عليها بواسطة راسم الذبذبات

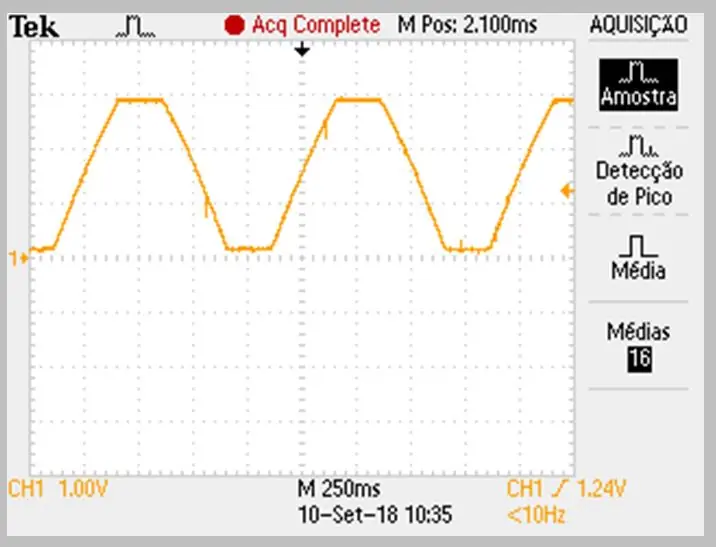
تم تنفيذ صورة الالتقاط بواسطة مرسمة الذبذبات. تم تخزين البيانات في ملف csv. لاحظ الانحناء الطفيف على منحدرات الإشارة الصاعدة والهابطة.

الخطوة 7: البيانات التي تم الحصول عليها بواسطة راسم الذبذبات (ملف csv في Excel)

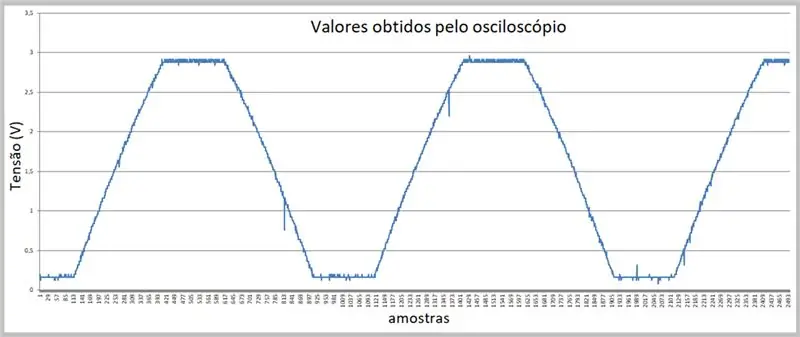
لدينا عينات هنا.

الخطوة 8: البيانات التي حصلت عليها ADC

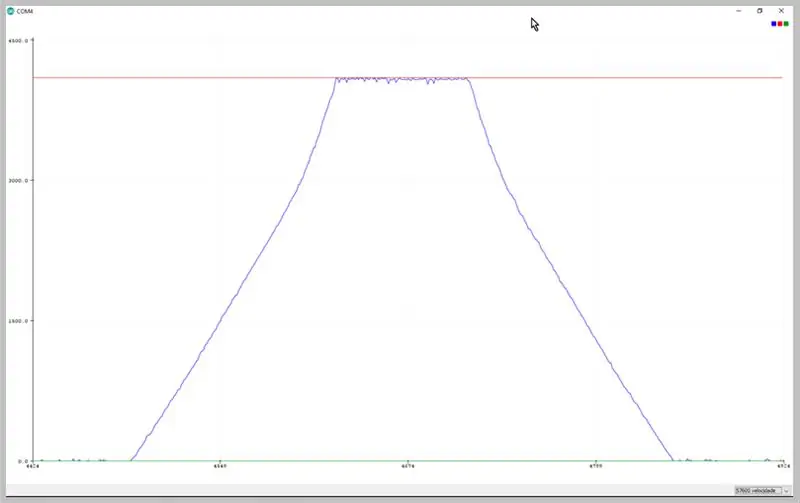
من خلال تغيير معدل نقل المسلسل ، يمكننا عرض البيانات التي تم التقاطها بواسطة ADC. لاحظ تشوه إشارة شبه منحرف.

البيانات التي لوحظت على الراسمة التسلسلية Arduino IDE

الخطوة 9: البيانات التي تم الحصول عليها بواسطة ADC - Excel

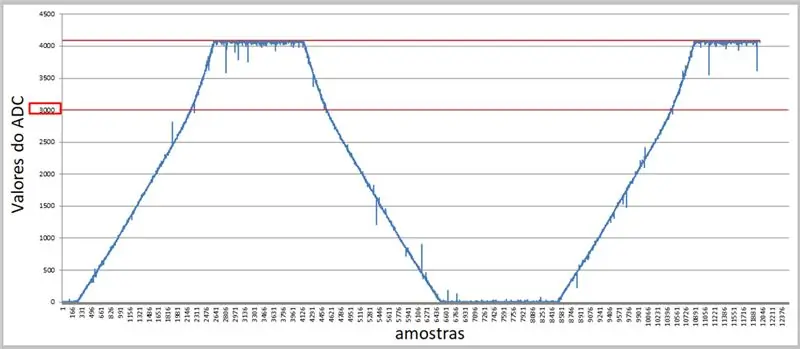
باستخدام معدل أعلى ومحطة تسلسلية ، يمكننا التقاط القيم وتطبيقها في Excel لمقارناتنا.

الخطوة 10: مقارنة منحدرات التسلق

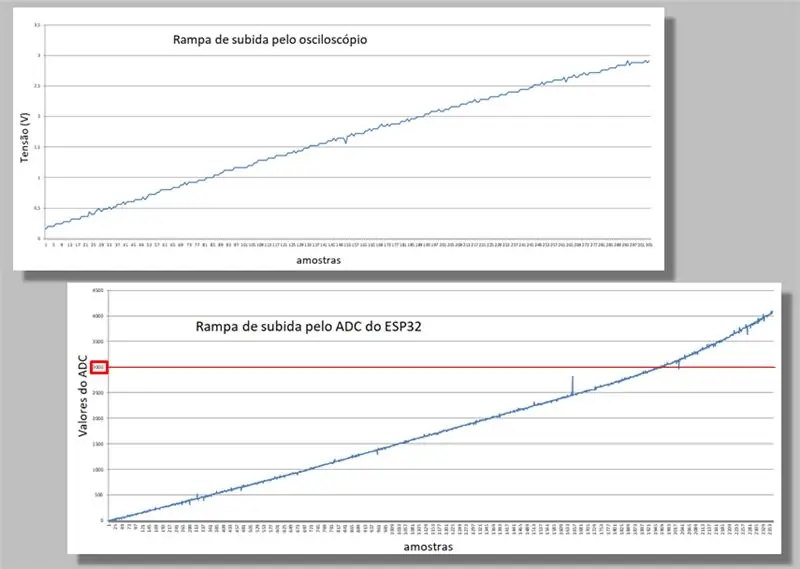
قارنا بين منحدرين للتسلق للمسكين.

لاحظ الانحناء الذي يحدث على كلا المنحدرين.

لاحظ أيضًا أنه بالنسبة للمنحدر نفسه ، لدينا العديد من عينات ESP32 أكثر من عينات الذبذبات.

الخطوة 11: معادلة عدد العينات

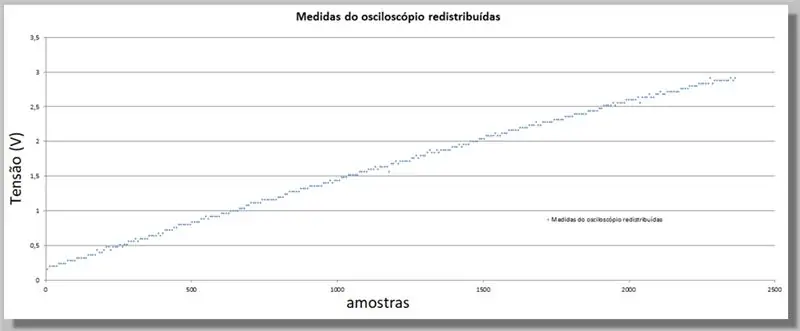
نظرًا لأن ESP32 قدم عددًا أكبر من العينات من راسم الذبذبات ، فإننا نحتاج إلى مساواة هذه القيم ، حيث إنها ستكون بمثابة مؤشر لمقارنة المنحنيين.

لهذا ، سنقوم بإجراء مقارنة مباشرة.

لدينا 305 عينة لمنحدر الذبذبات و 2365 عينة لمنحدر ADC.

نظرًا لأن المنحدرات من نفس النطاق ، يمكننا القول أن لدينا ما يقرب من 7.75 عينة من ADC لكل راسم ذبذبات.

ضرب مؤشر كل عينة من راسم الذبذبات له نفس المنحنى ، ولكن مع مؤشرات مكافئة لـ ADC والبيانات المعاد توزيعها.

لملء البيانات المفقودة للوظائف الجديدة ، سنطبق منحنى يناسب البيانات المعروفة إحصائيًا.

الخطوة 12: سد الثغرات - خط الاتجاه

تحديد البيانات المعروفة (النقاط الزرقاء) ، بالنقر ثم النقر بالزر الأيمن ، نختار: "إضافة خط الاتجاه …"

في النافذة التي تظهر ، نختار نوع متعدد الحدود (سيكون الطلب 2 كافيًا).

قمنا أيضًا بالتحقق من الخيارين "عرض المعادلة في الرسم البياني" و "عرض قيمة مربع R في الرسم البياني".

نضغط على "إغلاق".

الخطوة 13: سد الثغرات - منحنى متعدد الحدود من الدرجة 2

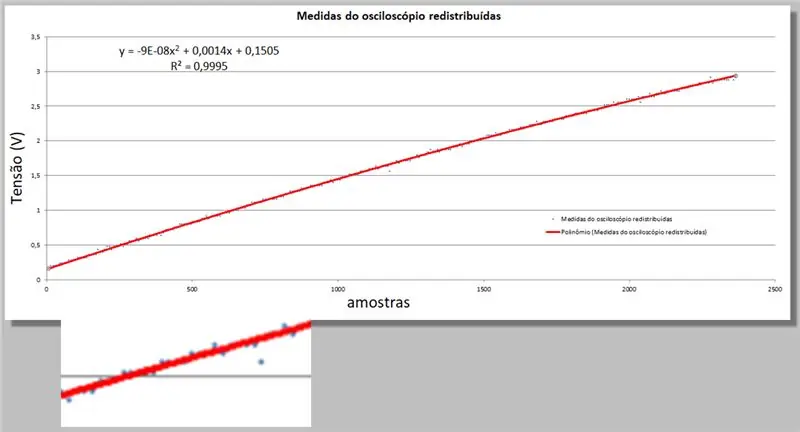
يمنحنا Excel معلومتين جديدتين ؛ معادلة الدرجة الثانية التي تناسب البيانات بشكل أفضل ، ومعادلة R التربيعية التي تحدد هذه الملاءمة.

فقط تذكر أنه كلما اقتربنا من 1 ، كانت المعادلة أكثر ملاءمة.

دعونا لا نتعمق في الرياضيات المتضمنة ، دعنا نستخدمها فقط كأداة.

الخطوة 14: سد الثغرات - تقييم الوظيفة

دعنا نملأ فجوات العينات بالبيانات الناتجة عن المعادلة. ثم قارنهم نقطة بنقطة.

ص = -9E-08x2 + 0 ، 0014x + 0 ، 1505

R² = 0 ، 9999

جهد راسم الذبذبات = -9E-08 * index2 + 0 ، 0014 * index + 0 ، 1505

الخطوة 15: تحويل جهد راسم الذبذبات إلى قيمة مكافئة للمقارنة مع ADC

دعنا نستفيد من هذا أيضًا لتحويل قيمة جهد راسم الذبذبات إلى قيمة ADC مكافئة.

نظرًا لأن أعلى قيمة تم الحصول عليها في ADP لـ ESP32 كانت 4095 ، أي ما يعادل قراءة 2.958 فولت لنفس الفهرس ، يمكننا القول:

يساوي كل فولت في قياسات الذبذبات 1384.4 وحدة تقريبًا من AD. لذلك ، يمكننا ضرب جميع قياسات الذبذبات في هذه القيمة.

الخطوة 16: مقارنة المنحدرين اللذين تم الحصول عليهما

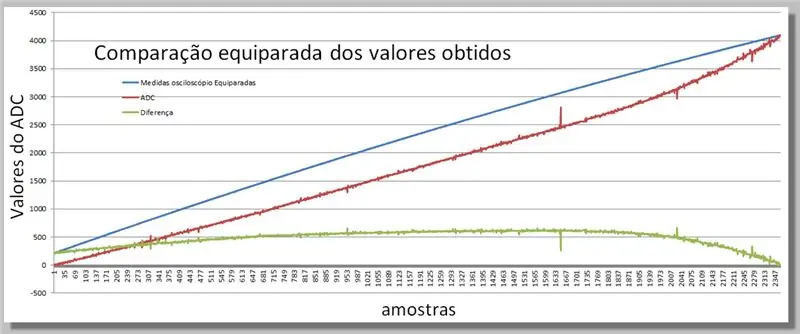
تصور الفروق التي تم الحصول عليها في القراءتين.

الخطوة 17: سلوك اختلاف القراءة ADC (خطأ)

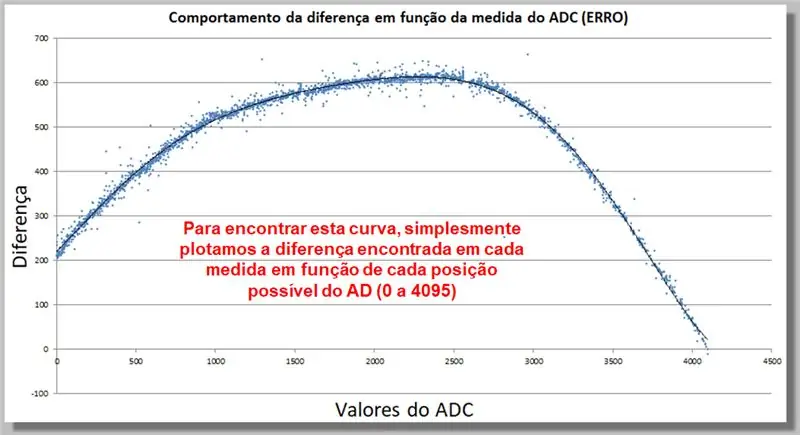
يوضح المنحنى أدناه كيف يتصرف الاختلاف في قراءة ADC كدالة للقياس. ستسمح لنا مجموعة البيانات هذه بالعثور على وظيفة تصحيح.

لإيجاد هذا المنحنى ، نرسم ببساطة الفرق الموجود في كل مقياس كدالة لكل موضع AD ممكن (من 0 إلى 4095).

الخطوة 18: سلوك اختلاف القراءة ADC - إيجاد وظيفة تصحيح

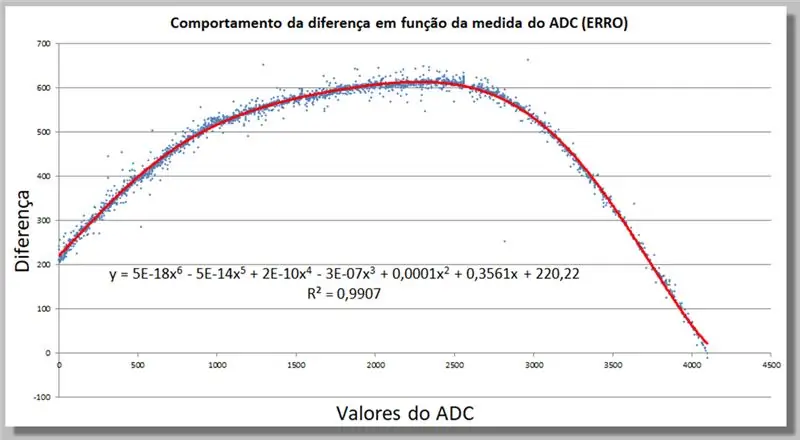
يمكننا تحديد وظيفة تصحيح في Excel عن طريق إضافة خط اتجاه ، الآن بدرجة أعلى ، حتى يتناسب بشكل كاف مع بياناتنا.

الخطوة 19: استخدام برامج أخرى

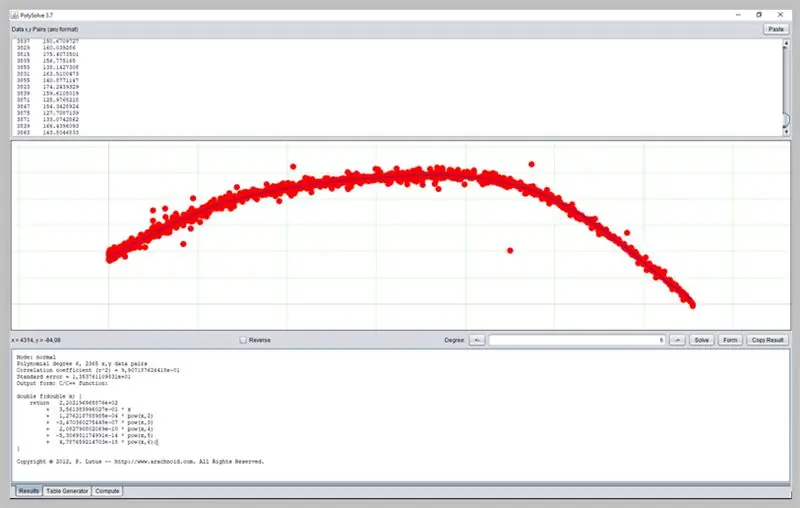
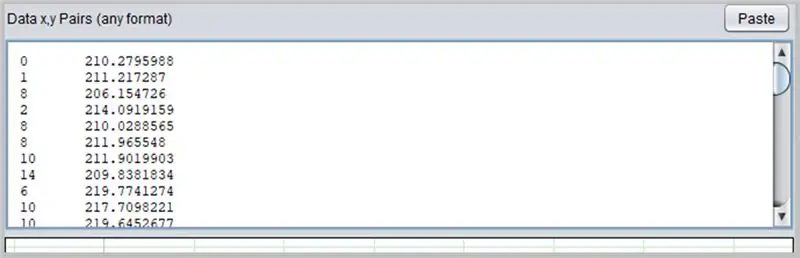
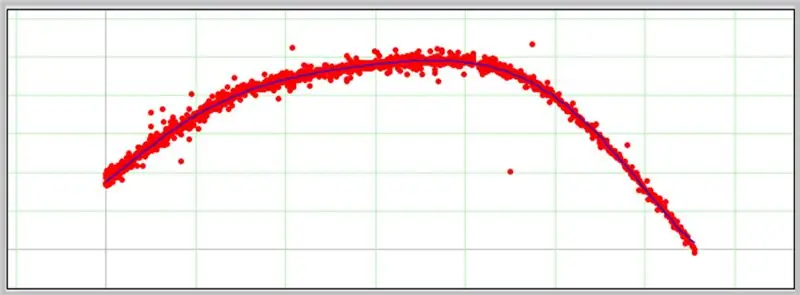
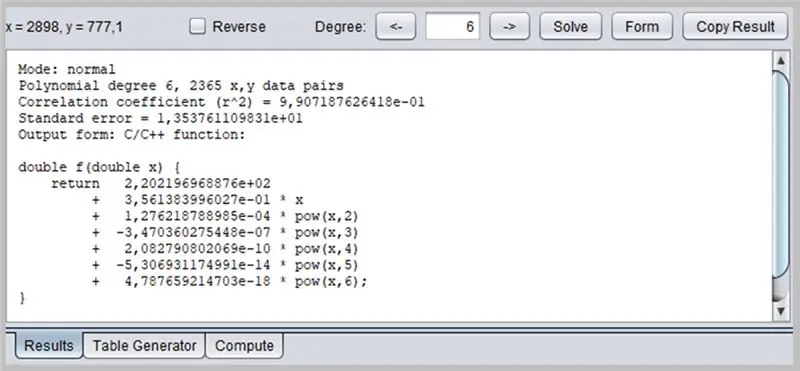
برنامج آخر مثير للاهتمام لتحديد المنحنيات هو PolySolve ، والذي يمكن استخدامه مباشرة على الرابط: https://arachnoid.com/polysolve/ أو تنزيله كتطبيق Java.

يسمح بتطبيق انحدار متعدد الحدود عالي الدرجات وتقديم الوظيفة المنسقة ، بالإضافة إلى وظائف أخرى.

لاستخدامه ، ما عليك سوى إدخال البيانات في مربع النص الأول. يجب أن تتبع البيانات الترتيب X أو Y مفصولاً بفاصلة أو علامة تبويب. كن حذرًا عند استخدام النقطة بشكل صحيح كنقطة عشرية.

سيظهر مخطط في المربع التالي إذا تم تنسيق البيانات المدخلة بشكل صحيح.

إليك كيف ذهب منحنى خطأ ADC الخاص بنا.

ستعرض هذه النافذة نتيجة الانحدار ، بما في ذلك بيانات كفاية الوظيفة ، والتي بدورها يمكن أن يتم تنسيق مخرجاتها بعدة طرق: كدالة C / C ++ ، وقائمة من المعاملات ، ودالة مكتوبة بلغة Java ، إلخ.

ملاحظة: انتبه إلى الفواصل العشرية

الخطوة 20: الثوابت والإعداد ()

أشير هنا إلى GPIO المستخدمة في الالتقاط التناظري. أقوم بتهيئة المنفذ التسلسلي ، بالإضافة إلى الدبوس المحدد للالتقاط التناظري.

const int pin_leitura = 36 ؛ // GPIO usado para captura analógica void setup () {Serial.begin (1000000) ؛ // Iniciciando a porta serial somente para debug pinMode (pin_leitura ، INPUT) ؛ // Pino utilizado para captura analógica}

الخطوة 21: حلقة () ووظيفة التصحيح

نقوم بالتقاط الجهد المضبوط ، ونطبع القيم بالتصحيحات الصحيحة أو بدونها.

حلقة فارغة () {int valor_analogico = analogRead (pin_leitura) ؛ // realiza a captura da tensão ajustada //Serial.print(valor_analogico + f (valor_analogico)) ؛ // Imprime os valores para debug (COM CORREÇOO) Serial.print (valor_analogico) ؛ // Imprimime os valores para debug (SEM CORREÇO) Serial.print ("،")؛ Serial.print (4095) ؛ // cria uma linha para marcar o valor máximo de 4095 Serial.print ("،") ؛ Serial.println (0) ، // cria uma linha para marcar o valor mínimo de 0}

لاحظ في السطر 12 أن لدينا خيار طباعة البيانات مع إضافة وظيفة الاختلاف f (analog_value).

الخطوة 22: استخدام وظيفة التصحيح PolySolve

هنا ، نستخدم وظيفة PolySolve داخل Arduino IDE.

/ * الوضع: متعدد الحدود العادي 6 ، 2365 x ، y أزواج البيانات معامل الارتباط (r ^ 2) = 9 ، 907187626418e-01 الخطأ القياسي = 1 ، 353761109831e + 01 نموذج الإخراج: وظيفة C / C ++: حقوق النشر © 2012 ، P. لوتس - https://www.arachnoid.com. كل الحقوق محفوظة. * / double f (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x، 2) + -3.470360275448e-07 * pow (x، 3) + 2.082790802069e- 10 * الأسرى (س ، 4) + -5.306931174991e-14 * الأسرى (س ، 5) + 4.787659214703e-18 * الأسرى (س ، 6) ؛ }

لاحظ تغيير الفاصلة بنقطة كفاصل عشري.

الخطوة 23: الالتقاط مع التصحيح - المسلسل الراسمة

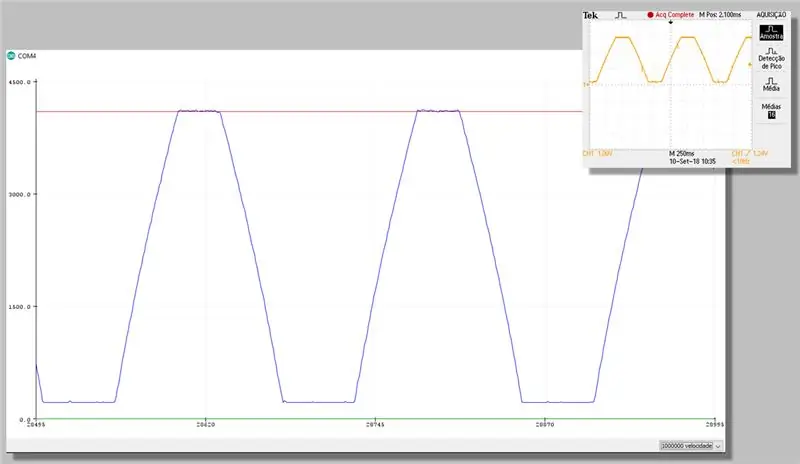
الخطوة 24: التكلفة الحسابية

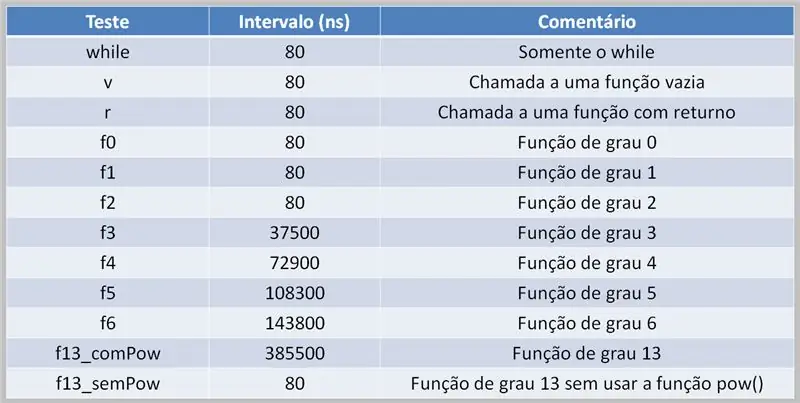
لإجراء حسابات كثيرة الحدود ، من الضروري أن يتولى المعالج هذه المهمة. يمكن أن يؤدي ذلك إلى تأخيرات في التنفيذ ، اعتمادًا على كود المصدر وقوة الحوسبة المتاحة.

هنا ، نرى جدول نتيجة اختبار يستخدم متعدد الحدود متعدد الدرجات. لاحظ الفرق بين الأوقات التي تم فيها استخدام الوظيفة pow () ومتى لم تكن كذلك.

الخطوة 25: رمز الاختبار - الإعداد () وبدء الحلقة ()

هنا ، لدينا الكود المستخدم في اختبارنا.

إعداد باطل () {Serial.begin (1000000) ؛ // Iniciando a porta serial somente para debug} حلقة فارغة () {float valor_analogico = 500.0؛ // um valor arbtrario float quantidade = 10000.0 ؛ // quantidade de chamadas float contador = 0.0 ؛ // كونتادور دي تشاماداس

الخطوة 26: رمز الاختبار - الحلقة () والمعالجة

لقد استخدمت الدالة micros () للحصول على القيمة بالميكروثانية.

// ============== inicia o processo float agora = micros () ؛ // marca o instante inicial while (contador <quantidade) {// v (valor_analogico) ؛ // função vazia // r (valor_analogico) ؛ // função com retorno // f0 (valor_analogico) ؛ // grau 0 // f1 (valor_analogico) ؛ // grau 1 // f2 (valor_analogico) ؛ // grau 2 // f3 (valor_analogico) ؛ // grau 3 // f4 (valor_analogico) ؛ // grau 4 // f5 (valor_analogico) ؛ // grau 5 // f6 (valor_analogico) ؛ // grau 6 // f13_semPow (valor_analogico) ؛ // grau 13º SEM a função POW // f13_comPow (valor_analogico) ؛ // grau 13º COM a função POW contador ++ ؛ } agora = (micros () - agora) / quantidade ؛ // Determina o interalo que se passou para cada iteração // ============= finaliza o processo

الخطوة 27: رمز الاختبار - الحلقة () - النتائج

نقوم بطباعة القيمة التي تم إرجاعها من وظيفة الصف 13 مع وبدون أسير الحرب للمقارنة ، بالإضافة إلى الفاصل الزمني للمعالجة.

// Imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)) ؛ // grau 13º SEM a função POW Serial.print ("-") ؛ Serial.print (f13_comPow (valor_analogico)) ؛ // grau 13º COM a função POW Serial.print ("-") ؛ // Imprime o interalo do processo Serial.println (agora، 6) ؛ }

الخطوة 28: رمز الاختبار - الوظائف المستخدمة

دوال فارغة (فقط مع الإرجاع) من الدرجة 0 و 1.

// FUNÇÃO VAZIAdouble v (double x) {} // FUNÇÃO SOMENTE COM RETORNO double r (double x) {return x؛ } // FUNÇÃO DE GRAU 0 double f0 (double x) {return 2.202196968876e + 02 ؛ } // FUNÇÃO DE GRAU 1 double f1 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x ؛ }

وظائف الصف 2 و 3 و 4.

// FUNÇÃO DE GRAU 2double f2 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x، 2) ؛ } // FUNÇÃO DE GRAU 3 double f3 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x، 2) + -3.470360275448e-07 * pow (x، 3) ؛ } // FUNÇÃO DE GRAU 4 double f4 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x، 2) + -3.470360275448e-07 * pow (x، 3) + 2.082790802069e-10 * الأسرى (س ، 4) ؛ }

وظائف الصف 5 و 6.

// FUNÇÃO DE GRAU 5double f5 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x، 2) + -3.470360275448e-07 * pow (x، 3) + 2.082790802069e-10 * pow (x ، 4) + -5.306931174991e-14 * pow (x ، 5) ؛ } // FUNÇÃO DE GRAU 6 double f6 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x، 2) + -3.470360275448e-07 * pow (x، 3) + 2.082790802069e-10 * pow (x، 4) + -5.306931174991e-14 * pow (x، 5) + 4.787659214703e-18 * pow (x، 6) ؛ }

وظيفة الصف 13 باستخدام POW.

// FUNÇÃO DE GRAU 13 USANDO O POW مزدوج f13_comPow (مزدوج x) {return 2، 161282383460e + 02 + 3، 944594843419e-01 * x + 5، 395439724295e-04 * pow (x، 2) + -3، 968558178426e-06 * pow (x، 3) + 1، 047910519933e-08 * pow (x، 4) + -1، 479271312313e-11 * pow (x، 5) + 1، 220894795714e-14 * pow (x، 6) + -6، 136200785076e-18 * pow (x، 7) + 1، 910015248179e-21 * pow (x، 8) + -3، 566607830903e-25 * pow (x، 9) + 5، 000280815521e-30 * pow (x، 10) + 3 ، 434515045670e-32 * pow (x ، 11) + -1 ، 407635444704e-35 * pow (x ، 12) + 9 ، 871816383223e-40 * pow (x ، 13) ؛ }

وظيفة الصف 13 بدون استخدام POW.

// FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow (double x) {return 2، 161282383460e + 02 + 3، 944594843419e-01 * x + 5، 395439724295e-04 * x * x + -3، 968558178426e-06 * x * x * x + 1، 047910519933e-08 * x * x * x * x + -1، 479271312313e-11 * x * x * x * x * x + 1، 220894795714e-14 * x * x * x * x * x * x + -6، 136200785076e-18 * x * x * x * x * x * x * x + 1، 910015248179e-21 * x * x * x * x * x * x * x * x + -3، 566607830903e- 25 * x * * x * x * x * x * x * x * x + 5، 000280815521e-30 * x * x * x * x * x * x * x * x * x + 3، 434515045670e- 32 * x * * x * x * x * x * x * x * x * x * x + -1، 407635444704e-35 * x * x * x * x * x * x * x * x * x * x * x + 9 ، 871816383223e-40 * x * x * x * x * x * * x * x * x * x * x * x * x ؛ }

الخطوة 29: الملفات

قم بتنزيل الملفات:

بي دي إف

انا لا

جدول