
جدول المحتويات:
- مؤلف John Day [email protected].
- Public 2024-01-30 07:40.
- آخر تعديل 2025-01-23 12:54.

في الآونة الأخيرة ، تم إنجاز الكثير من العمل في الموازنة الذاتية للأشياء. بدأ مفهوم التوازن الذاتي بموازنة البندول المقلوب. امتد هذا المفهوم ليشمل تصميم الطائرات أيضًا. في هذا المشروع ، صممنا نموذجًا صغيرًا للروبوت ذاتي التوازن باستخدام خوارزمية PID (التناسبية والتكاملية والمشتقة). منذ ذلك الحين ، أصبحت هذه الطريقة هي الوجه الجديد لأنظمة التحكم في العمليات الصناعية. يستعرض هذا التقرير الأساليب المتبعة في الموازنة الذاتية للكائنات. تم إجراء هذا المشروع كمشروع فصل دراسي لفهم ارتباط PID بكفاءة العمليات الصناعية المختلفة. نحن هنا نركز فقط على تقديم مراجعة موجزة عن فعالية وتطبيق عنصر التحكم PID. تم تطوير هذه الورقة من خلال تقديم مقدمة موجزة لأنظمة التحكم والمصطلحات ذات الصلة ، بالإضافة إلى دوافع المشروع. تم إجراء التجارب والملاحظات ، ووصف المزايا والعيوب مع الانتهاء عند التحسينات المستقبلية. تم تطوير نموذج للروبوت ذاتي التوازن لفهم فعالية PID في عالم نظام التحكم. بعد إجراء بعض الاختبارات والتجارب الصارمة ، تم اكتشاف مزايا وعيوب نظام التحكم PID. وجد أنه على الرغم من العديد من مزايا التحكم في PID على الطرق السابقة ، لا يزال هذا النظام يتطلب الكثير من التحسينات. من المأمول أن يحصل القارئ على فهم جيد لأهمية التوازن الذاتي وفعالية التحكم في PID وعجزه.
الخطوة 1: مقدمة
مع ظهور أجهزة الكمبيوتر وتصنيع العمليات ، عبر تاريخ الإنسان ، كان هناك دائمًا بحث لتطوير طرق لإعادة العمليات والأهم من ذلك ، للتحكم فيها باستخدام الآلات بشكل مستقل. والغرض من ذلك هو تقليل مشاركة الإنسان في هذه العمليات ، وبالتالي تقليل الخطأ في هذه العمليات. ومن هنا تم تطوير مجال "هندسة أنظمة التحكم". يمكن تعريف هندسة أنظمة التحكم على أنها تستخدم طرقًا مختلفة للتحكم في عمل العملية أو الحفاظ على بيئة ثابتة ومفضلة ، سواء أكانت يدوية أم تلقائية.
من الأمثلة البسيطة على ذلك التحكم في درجة الحرارة في الغرفة. يعني التحكم اليدوي وجود شخص في الموقع يقوم بفحص الظروف الحالية (المستشعر) ، ويقارنها بالقيمة المطلوبة (المعالجة) ويتخذ الإجراء المناسب للحصول على القيمة المطلوبة (المشغل). المشكلة في هذه الطريقة أنها غير موثوقة للغاية حيث أن الشخص عرضة للخطأ أو الإهمال في عمله. أيضًا ، هناك مشكلة أخرى تتمثل في أن معدل العملية التي بدأها المشغل ليس دائمًا موحدًا ، مما يعني أنه في بعض الأحيان قد يحدث بشكل أسرع من المطلوب أو قد يكون بطيئًا في بعض الأحيان. كان حل هذه المشكلة هو استخدام وحدة تحكم صغيرة للتحكم في النظام. المتحكم الجزئي
مبرمجة للتحكم في العملية ، وفقًا لمواصفات معينة ، متصلة في دائرة (ستتم مناقشتها لاحقًا) ، تغذي القيمة أو الشروط المطلوبة وبالتالي تتحكم في العملية للحفاظ على القيمة المطلوبة. ميزة هذه العملية هي أنه لا يوجد تدخل بشري مطلوب في هذه العملية. أيضا ، معدل العملية موحد
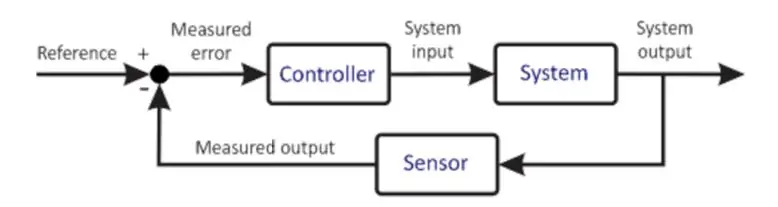
نظام التحكم الأساسي
يوضح الرسم البياني السابق نسخة مبسطة للغاية من نظام التحكم. يعتبر الميكروكونترولر في قلب أي نظام تحكم. إنه عنصر مهم للغاية ، لذلك يجب أن يتم اختياره بعناية بناءً على متطلبات النظام. تستقبل وحدة التحكم الدقيقة مدخلات من المستخدم. يحدد هذا الإدخال الحالة المرغوبة للنظام. تستقبل وحدة التحكم الدقيقة أيضًا مدخلات تغذية مرتدة من المستشعر. يتصل هذا المستشعر بإخراج النظام ، حيث يتم إعادة المعلومات الخاصة به إلى المدخلات. يقوم المعالج الدقيق ، بناءً على برمجته ، بإجراء حسابات مختلفة ويعطي ناتجًا للمشغل. يتحكم المشغل ، بناءً على الإخراج ، في المصنع لمحاولة الحفاظ على هذه الظروف. مثال على ذلك يمكن أن يكون سائق محرك يقود محركًا حيث يكون سائق المحرك هو المشغل والمحرك هو المصنع. وبالتالي يدور المحرك بسرعة معينة. يقوم المستشعر المتصل بقراءة حالة المصنع في الوقت الحالي وإعادته إلى وحدة التحكم الدقيقة. وحدة التحكم الصغيرة تقارن مرة أخرى ، وتقوم بالحسابات ، وبالتالي ، فإن الدورة تكرر نفسها. هذه العملية متكررة ولا نهاية لها حيث تحافظ وحدة التحكم الدقيقة على الظروف المطلوبة
الخطوة 2: نظام التحكم القائم على PID
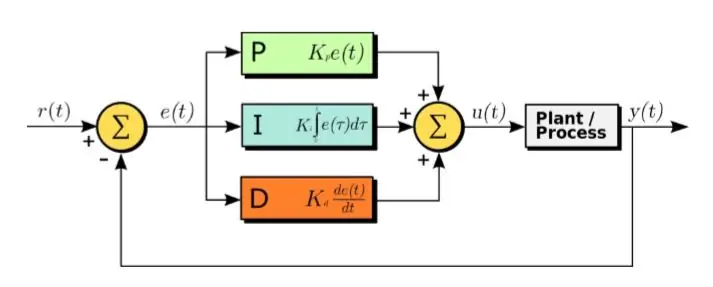

تعد خوارزمية PID طريقة فعالة لتصميم نظام تحكم.
التعريف
يرمز PID إلى النسبي والتكامل والمشتق. في هذه الخوارزمية ، إشارة الخطأ المتلقاة هي المدخلات. ويتم تطبيق المعادلة التالية على إشارة الخطأ
U (t) = Kp ∗ e (t) + Kd ∗ d / dt (e (t)) + Ki ∗ لا يتجزأ (e (t)) (1.1)
شرح موجز
كما يتضح من المعادلة أعلاه ، يتم حساب تكامل ومشتق إشارات الخطأ وضربها في الثوابت الخاصة بها وإضافتها مع الثابت Kp مضروبًا في e (t). ثم يتم تغذية الإخراج إلى المشغل الذي يجعل النظام يعمل. الآن دعنا نلقي نظرة على كل جزء من الوظيفة بدوره. تؤثر هذه الوظيفة بشكل مباشر على وقت الصعود ووقت السقوط والذروة فوق التصوير ووقت الاستقرار وخطأ الحالة المستقر.
• الجزء النسبي: يقلل الجزء المتناسب من وقت الصعود ويقلل من خطأ الحالة المستقرة. هذا يعني أن النظام سيستغرق وقتًا أقل للوصول إلى قيمته القصوى وعندما يصل إلى حالته المستقرة ، سيكون خطأ الحالة المستقرة منخفضًا. ومع ذلك ، فإنه يزيد من ذروة التجاوز.
• الجزء المشتق: الجزء المشتق يقلل من التجاوز ووقت الاستقرار. هذا يعني أن الحالة المؤقتة للنظام ستكون أكثر ثباتًا. أيضًا ، سيصل النظام إلى حالته المستقرة في وقت أقل. ومع ذلك ، ليس لها أي تأثير على وقت الصعود أو خطأ الحالة المستقرة.
• الجزء المتكامل: يقلل الجزء المتكامل من وقت الصعود ويزيل خطأ الحالة المستقرة تمامًا. ومع ذلك ، فإنه يزيد من ذروة التجاوز ووقت الاستقرار.
• الضبط: سيكون لنظام التحكم الجيد وقت صعود منخفض ، ووقت استقرار ، وتجاوز ذروة ، وخطأ ثابت في الحالة. لذلك ، يجب ضبط Kp و Kd و Ki بدقة لضبط مساهمة العوامل المذكورة أعلاه من أجل الحصول على نظام تحكم جيد.
تم إرفاق شكل يوضح تأثير تغيير المعلمات المختلفة في خوارزمية PID.
الخطوة الثالثة: روبوت ذاتي التوازن

الروبوت ذاتي التوازن هو روبوت متعدد الطبقات ذو عجلتين.
سيحاول الروبوت أن يوازن نفسه عند استخدام أي قوة (قوى) غير متكافئة. سوف يوازن نفسه عن طريق تطبيق القوة في مواجهة ناتج القوى على الروبوت.
طرق الموازنة الذاتية
هناك أربع طرق للموازنة الذاتية للروبوتات. هذه كالتالي:
موازنة ذاتية باستخدام مستشعرين للإمالة بالأشعة تحت الحمراء
هذه واحدة من أكثر الطرق فظاظة لموازنة الروبوت لأنها تتطلب أجهزة أقل وخوارزمية سهلة نسبيًا. في هذا النهج ، يتم استخدام مستشعرين مائلين بالأشعة تحت الحمراء لقياس المسافة بين الأرض والروبوت. بناءً على المسافة المحسوبة ، يمكن استخدام PID لقيادة المحركات لموازنة الروبوت وفقًا لذلك. أحد عيوب هذه الطريقة هو أن مستشعر الأشعة تحت الحمراء يمكن أن يغيب عن بعض القراءات. مشكلة أخرى هي أن المقاطعة والحلقات مطلوبة لحساب المسافة مما يزيد من التعقيد الزمني للخوارزمية. ومن ثم ، فإن طريقة موازنة الروبوت هذه ليست فعالة كثيرًا.
موازنة ذاتية باستخدام مقياس التسارع
مقياس التسارع يعطينا تسارع الجسم في 3 محاور. يعطينا التسارع الموجه في المحور y (لأعلى) والمحور x (للأمام) مقياسًا لحساب اتجاه الجاذبية ومن ثم حساب زاوية الميل. الزاوية تحسب على النحو التالي:
θ = arctan (Ay / Ax) (1.2)
عيب استخدام هذه الطريقة هو أنه أثناء حركة الروبوت ، سيتم أيضًا إضافة التسارع الأفقي إلى القراءات وهو ضوضاء عالية التردد. ومن ثم ، فإن زاوية الميل ستكون غير دقيقة.
الموازنة الذاتية باستخدام الجيروسكوب
يستخدم الجيروسكوب لحساب السرعات الزاويّة على طول المحاور الثلاثة. يتم الحصول على زاوية الميل باستخدام المعادلة التالية.
θp (i) = θp (i 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1.3)
أحد العيوب الكبيرة لاستخدام الجيروسكوب هو أنه يحتوي على انحياز صغير للتيار المستمر وهو عبارة عن ضوضاء منخفضة التردد وفي وقت قصير تكون القيم التي تم إرجاعها خاطئة تمامًا. هذا ، بعد التكامل ، سيؤدي إلى انحراف نقطة الصفر بعيدًا. نتيجة لذلك ، سيبقى الروبوت في وضعه الرأسي لبعض الوقت وسيسقط بمجرد أن يأتي الانجراف.
موازنة ذاتية باستخدام كل من مقياس التسارع والجيروسكوب
كما نوقش أعلاه ، فإن استخدام مقياس التسارع أو الجيروسكوب فقط لن يعطينا زاوية الميل الصحيحة. لحساب ذلك ، يتم استخدام كل من مقياس التسارع والجيروسكوب. كلاهما مضمن في MPU6050. في هذا نحصل على البيانات من كلاهما ثم ندمجها إما باستخدام مرشح كالمان أو مرشح التكميلي.
• مرشح كالمان: يحسب مرشح كالمان أفضل تقدير لحالة النظام الديناميكي من القياسات الصاخبة ، مما يقلل من متوسط الخطأ التربيعي للتقدير. يعمل على مرحلتين ، التنبؤ والتصحيح ، بالنظر إلى المعادلات العشوائية المنفصلة التي تصف ديناميكيات النظام. ومع ذلك ، فهي خوارزمية معقدة للغاية ليتم تنفيذها خاصة على أجهزة محدودة من متحكم دقيق.
• المرشح التكميلي: تستخدم هذه الخوارزمية بشكل أساسي البيانات التي تم الحصول عليها من الجيروسكوب وتدمجها بمرور الوقت للحصول على زاوية الميل. كما أنه يستخدم نسبة صغيرة من قراءات مقياس التسارع. في الواقع ، يقلل المرشح التكميلي من الضوضاء عالية التردد لمقياس التسارع وضوضاء التردد المنخفض للجيروسكوب ثم يدمجهما لإعطاء أفضل زاوية ميل دقيقة.
الخطوة 4: تصميم الروبوت
لقد صممنا روبوتًا ذاتي الموازنة باستخدام وحدة تحكم مشتقة متناسبة ينفذها مرشح تكميلي لـ MPU6050. سيوضح لنا هذا النموذج الصغير من روبوت التوازن الذاتي فائدة أنظمة التحكم في الموازنة الذاتية للروبوتات.
تنفيذ النظام:
النظام عبارة عن روبوت ذاتي التوازن. يتم تنفيذه باستخدام وحدة تحكم PID وهي وحدة تحكم مشتقة متكاملة نسبية. نحن نوازن الروبوت من خلال قيادة عجلاته في اتجاه سقوطه. عند القيام بذلك ، نحاول إبقاء مركز ثقل الروبوت فوق النقطة المحورية. لدفع العجلات في اتجاه سقوطها ، يجب أن نعرف مكان سقوط الروبوت والسرعة التي يسقط بها. يتم الحصول على هذه البيانات باستخدام MPU6050 الذي يحتوي على مقياس تسارع وجيروسكوب. يقيس MPU6050 زاوية الميل ويعطي ناتجه إلى وحدة التحكم الصغيرة. يتم توصيل MPU6050 بلوحة STM عبر I2C. في I2C ، يوجد سلك واحد للساعة التي تسمى SCL. الآخر هو لنقل البيانات وهو SDA. في هذا ، يتم استخدام اتصال الرقيق الرئيسي. يتم تحديد عنوان البداية وعنوان النهاية لمعرفة من أين تبدأ البيانات وأين تنتهي. لقد طبقنا هنا الفلتر التكميلي MPU6050 وهو مرشح رياضي لدمج مخرجات مقياس التسارع والجيروسكوب. بعد الحصول على البيانات من MPU6050 ، سيقوم المتحكم الدقيق بإجراء حسابات لمعرفة مكان سقوطه. بناءً على الحسابات ، ستعطي وحدة التحكم الدقيقة STM أوامر لسائق المحرك لقيادة المركبات في اتجاه السقوط الذي سيوازن الروبوت.
الخطوة 5: مكونات المشروع



تم استخدام المكونات التالية في مشروع الروبوت ذاتي التوازن:
STM32F407
وحدة تحكم دقيقة من تصميم ST Microelectronics. يعمل على معمارية ARM Cortex-M.
سائق موتور L298N
يستخدم هذا IC لتشغيل المحرك. يحصل على مدخلين خارجيين. واحد من الميكروكونترولر الذي يزوده بإشارة PWM. من خلال تعديل عرض النبض ، يمكن تعديل سرعة المحرك. الإدخال الثاني هو مصدر الجهد المطلوب لتشغيل المحرك وهو بطارية 12 فولت في حالتنا.
محرك DC
يعمل محرك DC على مصدر التيار المستمر. في هذه التجربة ، يتم تشغيل محرك التيار المستمر باستخدام optocouplers المتصلة بمحرك المحرك. لقيادة المحرك ، استخدمنا Motor Drive L298N.
MPU6050
يتم استخدام MPU6050 للحصول على معلومات حول مكان سقوط الروبوت. يقيس زاوية الميل فيما يتعلق بنقطة الميل الصفرية وهو موضع MPU6050 عند بدء تشغيل البرنامج.
يحتوي MPU6050 على مقياس تسارع ثلاثي المحاور وجيروسكوب ثلاثي المحاور. يقيس مقياس التسارع التسارع على طول المحاور الثلاثة ويقيس الجيروسكوب المعدل الزاوي حول المحاور الثلاثة. من أجل دمج المخرجات ، يجب علينا تصفية ضوضاء كليهما. لترشيح الضوضاء ، لدينا مرشح كالمان والمُكمِّل. لقد قمنا بتنفيذ برنامج تكميلي في مشروعنا.
زوجان البصريات 4N35
جهاز optocoupler هو جهاز يستخدم لعزل جزء الجهد المنخفض وجزء الجهد العالي من الدائرة. كما يوحي الاسم ، فهو يعمل على أساس الضوء. عندما يحصل جزء الجهد المنخفض على إشارة ، يتدفق التيار في جزء الجهد العالي
الخطوة 6: هيكل الروبوت
يتم شرح هيكل الروبوت على النحو التالي:
الهيكل المادي
يتكون الروبوت ذاتي التوازن من طبقتين مكونتين من زجاج بلاستيكي شفاف. فيما يلي تفاصيل طبقتين:
الطبقة الأولى
في الجزء السفلي من الطبقة الأولى ، وضعنا خلية لتشغيل لوحة STM. كما تم وضع محركين بجهد 4 فولت لكل جانب على كل جانب مع توصيل الإطارات للإنسان الآلي. في الجزء العلوي من الطبقة الأولى ، تم وضع بطاريتين 4 فولت لكل منهما (إجمالي 8 فولت) ومحرك محرك IC (L298N) لتشغيل المحركات.
الطبقة الثانية
في الطبقة العليا من الروبوت ، وضعنا لوح STM على لوح الأداء. يتم وضع لوحة أداء أخرى مكونة من 4 قارنات بصرية على الطبقة العليا. يتم وضع الجيروسكوب أيضًا على الطبقة العلوية للروبوت من الجانب السفلي. يتم وضع كلا المكونين في الجزء الأوسط بحيث يظل مركز الثقل منخفضًا قدر الإمكان.
مركز ثقل الروبوت
يتم الحفاظ على مركز الجاذبية عند أدنى مستوى ممكن. لهذا الغرض ، وضعنا بطاريات ثقيلة على الطبقة السفلية ومكونات خفيفة مثل لوحة STM ومقرنات ضوئية على الطبقة العليا.
الخطوة 7: الكود
تم تجميع الكود على Atollic TrueStudio. تم استخدام استوديو STM لأغراض التصحيح.
الخطوة 8: الخاتمة
بعد الكثير من التجارب والملاحظة ، وصلنا أخيرًا إلى النقطة التي نلخص فيها نتائجنا ونناقش إلى أي مدى نجحنا في تنفيذ فاعلية النظام والعمل عليها.
مراجعة عامة
أثناء التجربة ، تم التحكم في سرعة المحرك بنجاح باستخدام خوارزمية PID. ومع ذلك ، فإن المنحنى ليس بالضبط خطًا مستقيمًا سلسًا. وهناك أسباب كثيرة لذلك:
• على الرغم من توصيل المستشعر بمصفاة تمرير منخفضة ، إلا أنه لا يزال يوفر تنبيهات نهائية معينة ؛ هذه بسبب المقاومة غير الخطية وبعض الأسباب الحتمية للإلكترونيات التناظرية.
• لا يدور المحرك بسلاسة تحت الجهد المنخفض أو PWM. إنه يوفر هزات قد تسبب تغذية بعض القيم الخاطئة للنظام.
• بسبب التذبذب ، قد يفوت المستشعر بعض الشقوق التي توفر قيمًا أعلى. • يمكن أن يكون السبب الرئيسي الآخر للأخطاء هو تردد الساعة الأساسي لوحدة التحكم الدقيقة STM. يوفر هذا النموذج من متحكم STM ساعة أساسية تبلغ 168 ميجاهرتز. على الرغم من التعامل مع هذه المشكلة في هذا المشروع ، إلا أن هناك فكرة عامة حول هذا النموذج أنه لا يوفر مثل هذا التردد العالي بالضبط.
توفر سرعة الحلقة المفتوحة خطًا سلسًا للغاية مع عدد قليل من القيم غير المتوقعة. تعمل خوارزمية PID أيضًا على توفير وقت استقرار منخفض جدًا للمحرك. تم اختبار خوارزمية PID للمحرك تحت الفولتية المختلفة مع الحفاظ على السرعة المرجعية ثابتة. لا يغير تغيير الجهد من سرعة المحرك مما يدل على أن خوارزمية PID تعمل بسرعة
E وما يليها ectiveness
نناقش هنا فعالية وحدة تحكم PID التي لاحظناها أثناء التجربة.
تنفيذ بسيط
لقد رأينا في قسم التجارب والملاحظات أن وحدة تحكم PID سهلة التنفيذ للغاية. لا يتطلب سوى ثلاثة معلمات أو ثوابت يجب تعيينها من أجل الحصول على نظام للتحكم في السرعة
كفاءة لا مثيل لها للأنظمة الخطية
تعتبر وحدة التحكم الخطية PID هي الأكثر كفاءة في عائلة وحدات التحكم لأن المنطق بسيط للغاية والتطبيق واسع الانتشار في حالة التطبيقات الخطية أو الخطية إلى حد ما.
القيود
شرحنا في الملخص حدود هذا النظام. هنا نناقش القليل منها الذي لاحظناه.
اختيار الثوابت
لقد رأينا أنه على الرغم من سهولة تنفيذ وحدة التحكم PID ، إلا أنه لا يزال من العوائق الرئيسية للنظام أن خطوة اختيار قيمة الثوابت هي خطوة شاقة ؛ حيث يتعين على المرء إجراء حسابات صعبة. الطريقة الأخرى هي طريقة الضرب والمحاكمة ولكنها ليست فعالة أيضًا.
الثوابت ليست دائما ثابتة
أظهرت النتائج التجريبية أنه بالنسبة للقيم المختلفة للسرعة المرجعية للمحرك ، فإن وحدة التحكم PID معطلة لنفس قيم ثوابت PID. بالنسبة للسرعات المختلفة ، كان لا بد من تحديد الثوابت بشكل مختلف وهذا يزيد التكلفة الحسابية أضعافا مضاعفة.
غير خطي
وحدة التحكم PID المستخدمة في حالتنا خطية ، وبالتالي ، يمكن تطبيقها على الأنظمة الخطية فقط. بالنسبة للأنظمة غير الخطية ، يجب تنفيذ وحدة التحكم بشكل مختلف. على الرغم من توفر طرق غير خطية مختلفة لـ PID ، إلا أنها تتطلب المزيد من المعلمات ليتم اختيارها. هذا مرة أخرى يجعل النظام غير مرغوب فيه بسبب التكلفة الحسابية العالية.
الدفع الأولي مطلوب
لقد أوضحنا في قسم التجارب أنه بالنسبة لسرعة مرجعية صغيرة إلى حد ما حيث يكون الخطأ صغيرًا إلى حد ما في البداية ، فإن PWM الذي يوفره PID صغير جدًا بحيث لا يولد عزم الدوران المطلوب للمحرك. لذلك لا يعمل المحرك في بعض التجارب أو في التجارب الأخرى يوفر تجاوزًا كبيرًا ووقت استقرار أطول.
الخطوة 9: شكر خاص
شكر خاص لأعضاء مجموعتي الذين ساعدوني من خلال هذا المشروع.
سأقوم بتحميل رابط الفيديو قريبا.
آمل أن تجد هذه التعليمات ممتعة.
هذا توقيع طاهر الحق من UET. هتافات !!!
موصى به:
روبوت ذاتي التوازن - خوارزمية التحكم PID: 3 خطوات

روبوت التوازن الذاتي - خوارزمية التحكم PID: تم تصميم هذا المشروع لأنني كنت مهتمًا بمعرفة المزيد عن خوارزميات التحكم وكيفية التنفيذ الفعال لحلقات PID الوظيفية. لا يزال المشروع في مرحلة التطوير حيث لم تتم إضافة وحدة Bluetooth بعد والتي ستتم
روبوت ذاتي التوازن من ماجيكبيت: 6 خطوات

روبوت ذاتي التوازن من Magicbit: يوضح هذا البرنامج التعليمي كيفية صنع روبوت ذاتي التوازن باستخدام لوحة تطوير Magicbit. نحن نستخدم Magicbit كلوحة تطوير في هذا المشروع الذي يعتمد على ESP32. لذلك يمكن استخدام أي لوحة تطوير ESP32 في هذا المشروع
خوارزمية كورديك باستخدام VHDL: 4 خطوات
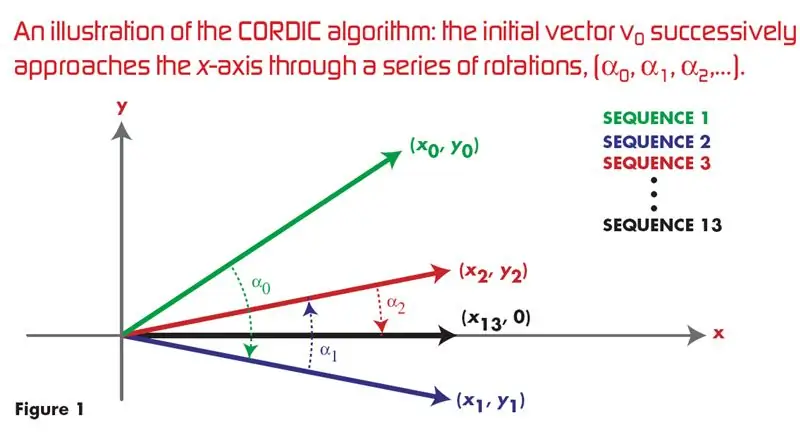
خوارزمية Cordic باستخدام VHDL: ## هذا هو الرابط الأكثر نقرًا وشائعًا في Google لتطبيق VHDL لـ CORDIC ALGORITHM لإنشاء موجة جيبية وجيب التمام ## في الوقت الحالي ، توجد العديد من الخوارزميات الفعالة للأجهزة ، ولكن هذه ليست معروفة جيدًا بسبب هيمنة البرامج
روبوت موازنة / روبوت ذو 3 عجلات / روبوت STEM: 8 خطوات

موازنة الروبوت / روبوت ذو 3 عجلات / روبوت STEM: لقد بنينا موازنة مجمعة وروبوت ثلاثي العجلات للاستخدام التعليمي في المدارس والبرامج التعليمية بعد المدرسة. يعتمد الروبوت على Arduino Uno ، وهو درع مخصص (يتم توفير جميع تفاصيل البناء) ، وحزمة بطارية Li Ion (جميعها
التحكم في سرعة محرك التيار المستمر باستخدام خوارزمية PID (STM32F4): 8 خطوات (بالصور)

التحكم في سرعة محرك التيار المستمر باستخدام خوارزمية PID (STM32F4): مرحبًا بالجميع ، هذا طاهر الحق مع مشروع آخر. هذه المرة هو STM32F407 كـ MC. هذا هو نهاية مشروع منتصف الفصل الدراسي. أتمنى أن تنال إعجابك ، فهي تتطلب الكثير من المفاهيم والنظريات ، لذلك نبدأ في ذلك أولاً ، مع ظهور أجهزة الكمبيوتر و
